Two New Algorithms for Radiation (Magneto-)Hydrodynamics Based on Solving the Specific Intensity Dir
- Jiang et al., 2012, ApJS, 199, 14; Davis et al.
- Jun 30, 2014
- 1 min read

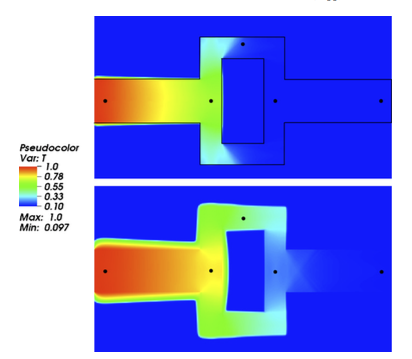
I have two different radiative transfer algorithms solving the radiation magneto-hydrodynamic equations self-consistently. Both methods do not assume any ad-hoc closure relation and they are accurate in both optically thick and optically thin regimes. They can work in both gas pressure dominated and radiation pressure dominated systems.
The first method ideal MHD equations explicitly plus the radiation moment equations implicitly.

The Eddington tensor is calculated based on the time-independent radiative transfer equation, which is solved with the short-characteristic method as described in Davis et al. (2012).

The radiation moment equations are solved implicitly over the whole methsh by inverting a matrix. Therefore, the time step is not limited by the time step. This method is most useful in catesian goemetry when the typical sound speed is much smaller than the speed of light.
The second algorithm is a completely new method which solves the following time dependent radiative transfer equation for specific intensity explicitly. There is no need to solve the radiation moment equation. The source term is first solved in the co-moving frame. Then all the velocity dependent terms are captured when the co-moving frame intensity I_0 are transformed to the lab-frame I via Lorentz transformation. Each specific intensity I is solved explicitly along angle n. The time step is limited by the speed of light. Therefore, the method is most useful when the typical flow velocity is not very small compared with the speed of light. If reduced speed of light can be used, this method is also very convenient to use, as it can be used in any coordinate system.
















Comments